Cuatro Plumas

la peregrinación del caballo

Durante siglos, matemáticos de todo el mundo han dedicado especial interés por esta serie de movimientos que conocemos como "peregrinación"; no pretendo ser uno de ellos, ni mucho menos parecer un tipo inteligente, porque no lo soy; soy mas bien un hombre ocioso que vive bajo la consigna "si él (ella) puede, yo también".

Obviamente, si tanta gente se ha dedicado ha estudiarlo, no consiste solo en pasear el caballo por un tablero con el fin de abarcar los 64 escaños, implica también buscar una lógica matemática-gráfica que haga de esto algo interesante; así, luego de probar varias combinaciones, esta es la que serie de movimientos que más me agradó; la hice solito, hoy a las 3:56 am...

Todo se origina a partir de un tablero se ajedrez simple (fig 1a), ahora bien, la clave de esta peregrinación y por ende, lo que la hace interesante, es su simetría; por esto he dividido el tablero en cuatro cuadrantes (azul, verde, rojo y gris, o bien, 1º, 2º, 3º y 4º respectivamente), los cuales serán visitados por el caballo siguiendo una dirección preestablecida, con dos giros en forma horaria y dos en forma antihoraria (fig 1b), de tal manera que por cada vez que una flecha se origine, visite o termine en alguno de los cuadrantes, el caballo realizará en él, 4 movimientos consecutivos. Los movimientos ejecutados en los cuadrantes 2º y 3º serán exactamente iguales para toda la peregrinación, tomando como casilleros de entrada y salida de dichos cuadrantes, aquellos que han sido resaltados en la fig 1c.
Partiré entonces con el primer giro antihorario (fig 2a), durante este primer recorrido, el caballo realizará cuatro movimientos por cuadrante, visitando aquellos casilleros que han sido resaltados en la fig 2b; se observa que en los cuadrantes 2º y 3º se originan 2 figuras romboidales exactamente iguales, mientras que en los cuadrantes 1º y 4º se forman figuras idénticas que resultan opuestas debido al distinto casillero de entrada que utilizamos para cada uno de ellos (mientras en el 1º iniciamos por el ángulo inferior derecho, en el 4º lo hacemos por el ángulo superior izquierdo). La fig 2c muestra el recorrido hasta ahora realizado, correspondiente al 25% del tablero.
Durante el segundo giro, esta vez en sentido horario (fig 3a), vemos que mientras en los cuadrantes 1º, 2º y 3º se originan rombos idénticos, en el 4º cuadrante se forma una figura romboidal (fig 3b). La fig 3c muestra el recorrido completado hasta este momento, correspondiente al 50% del tablero.
Para cuando se termina el tercer giro, realizado nuevamente en sentido horario (fig 4a), habremos originado 2 nuevos rombos idénticos en los cuadrantes 2º y 3º, mientras que en los cuadrantes 1º y 4º, se habrán formado figuras idénticas (fig 4b) que resultan distintas por el mismo principio ya explicado durante el primer giro (fig 2b); obsérvese que la imagen obtenida en el cuadrante 1º, corresponde a la obtenida en el 4º cuadrante durante el primer giro y viceversa. En este momento ya se ha recorrido el 75% del tablero (fig 4c).
Finalmente, se realiza el cuarto giro, esta vez en sentido antihorario (fig 5a), originando imágenes romboidales idénticas para los casilleros 1º, 2º y 3º (fig 5b), las cuales coinciden con la figura correspondiente al 4º casillero luego de haber realizado el segundo giro (fig 3b); además, durante el cuarto giro, en el 4º cuadrante se ha originado un rombo (fig 5b) idéntico a los presentados por los restantes 3 cuadrantes luego del segundo giro (fig 3b). La correspondencia entre estas figuras, proporciona la simetría del recorrido en cuestión. Para cuando alcancemos este punto, la peregrinación estará completa, es decir, el caballo habrá visitado los 64 casilleros del tablero (fig 5c).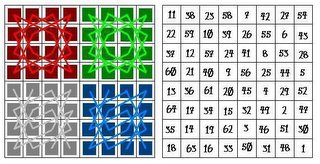
La fig 6a muestra los recorridos realizados en cada uno de los cuadrantes, se puede apreciar entonces, que las imágenes formadas en los casilleros 2º y 3º son idénticas entre si, como también lo son las originadas en los cuadrantes 1º y 4º.La fig 6b, por su parte, numera los 64 casilleros en el orden en el cual fueron visitados por el caballo; de esta forma, al realizar una simple operación matemática, es posible observar que la suma de los números correspondientes a cada fila y cada columna, es igual a 160, principio que se cumple para las 8 filas y 8 columnas que constituyen el tablero. Además, la suma de los números correspondientes a cada uno de los cuadrantes, es igual a 520.

Después de esta didáctica descripción, puedo concluir que para lograr esta serie de movimientos correlativos, hice trabajar como nunca a mi cabeza... y tal vez sea lo más idiota que haya escrito en mis 21 años de vida...

publicado por david @ 1:00 p. m.